- 3중슬릿 간섭
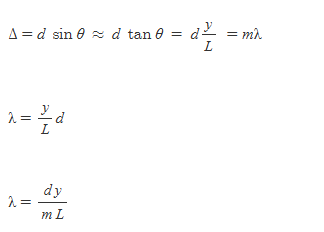
$\Delta =d\ \sin \theta \ \approx \ d\ \tan \theta \ =\ d\frac{y}{L}\ =m\lambda $Δ=d sinθ ≈ d tanθ = dyL =mλ
$\lambda =\frac{y}{L}d$λ=yLd
$\lambda =\frac{d\ y}{m\ L}$λ=d ym L
2. 박막간섭

$보강간섭\ \Delta \ =\ 2d=\frac{\lambda "}{2}\left(2m+1\right)$보강간섭 Δ = 2d=λ′2(2m+1)
$$
$\to d=\frac{\lambda }{4n}\left(2m+1\right)$→d=λ4n(2m+1)
$소멸간섭\Delta \ =\ 2d\ \ =\ \frac{\lambda }{2n}\left(2m\right)$소멸간섭Δ = 2d = λ2n(2m)
3. 단일슬릿 회전무늬
회절무늬간격 좁아지려면 d 커지고 L 작아지고 파장 작아져야함
> 격자 넓어지고 거리 줄어들고 파장이 짧아야
회절무늬 간격 넓어지려면
>격자d 좁아지고 L거리 멀어지고 파장 길어야

$\Delta =a\ \sin \theta $Δ=a sinθ
$보강\Delta \ =\ \frac{\lambda }{2}\left(2m+1\right)\ \to a\sin \theta =\lambda \left(2m+1\right)$보강Δ = λ2(2m+1) →asinθ=λ(2m+1)
$소멸\Delta \ =\ \frac{\lambda }{2}\left(2m\right)\ \to a\sin \theta =\lambda m\ \to a=\frac{\lambda }{\sin \theta }$소멸Δ = λ2(2m) →asinθ=λm →a=λsinθ
스넬의 굴절법칙 snell

$n\ \sin i\ =\ n"\ \sin i"$n sini = n′ sini′
v =c/굴절률n